Other Voting Systems · Fairer Representation

You never change things by fighting the existing reality. To change something, build a new model that makes the existing model obsolete.
Buckminster Fuller

1. Build consensus
2. Share
3. Treat everyone equally
4. Play nice

• Each interest group has their fair share of power
• Elected representatives are approved by the greatest possible number of voters
• Governing bodies reflect the diverse interests of those represented
• The greatest possible number of citizens have at least one sympathetic ear among their representatives
• Discussions among representatives reflect discussions among those represented
• In local elections, all voters to have a say about every city or county representative (no districts). By extension, all representatives are accountable to all voters.
• Voting without fear of unintended consequences or strategic voting dilemmas such as:
  • Fear of "wasting" a vote on a preferred candidate that many say can not win.
  • Inadvertently contributing to the election of the candidate a voter likes least by voting for a "long-shot" or other-party candidate.
  • Diluting the voting power of a party or interest group due to vote-splitting among several similar candidates.

• Reducing the cost of winning
• Discouraging negative campaigning
• Reducing the influence of gerrymandering

If you’re not satisfied with the results of past elections at all levels (local through national), remember the adage, "If you do what you’ve always done, you’ll get what you always got." Changes at the state and federal levels often begin with local reforms.

In many of our life decisions, we don’t just choose one option, and then let others choose for us if our top selection isn’t available. We prioritize items on our to-do lists. We make backup or contingency plans if our first effort doesn’t work out. If our first choice isn’t available, we expect the opportunity to make another selection from all the remaining options. If the ice cream store is out of our favorite flavor, we want to select an alternate from all the store’s flavors, not just the two flavors chosen most often by other customers. Why should we settle for less when we choose those who influence many aspects of our lives?

• The simplicity of a single election to determine the winner
• A familiar process regardless of the number of candidates
• The power to express your preference for every candidate

Ranked-choice voting (RCV), also known as Instant-Runoff Voting (IRV) or Single-Transferable Vote (STV), fulfills the above goals. In an RCV election, voters rank candidates in order of preference, much like prioritizing items on a to-do list. Voters who want to keep it simple can mark just one candidate and leave the other selections blank. Those who have nuanced opinions can express their preference for every candidate.

Primary elections ask voters "who is your most preferred candidate?". General or runoff elections ask, "Who is your most-preferred (or least-hated) candidate of those remaining?". RCV elections ask both questions on the same ballot. RCV uses the familiar process of a runoff between a reduced number of candidates but gets results with one election because voters are asked for their 2nd (and 3rd, 4th, etc.) choices on one ballot. Imagine multiple runoff elections with one less name on each runoff ballot but you only need to cast one ballot. The vote-counting computer has the information it needs to tabulate as many runoffs as required until one candidate gets over half of the votes. See the example below.

RCV has the obvious result of eliminating the need (and cost) of a separate runoff election if there’s no majority winner in the first round.

RCV builds consensus as voters who have their first-choice candidate eliminated in one round can choose a like-minded candidate in the next runoff round. A voting block with three candidates running will reach consensus on one of the three through multiple runoff rounds of vote counts. This eliminates problems due to multiple, similar candidates splitting the vote and unintentionally contributing to a win by a very different candidate.

"Long-shot" candidates will not affect the final outcome. If they really have few supporters, they will be eliminated in an early round and those who voted for them can cast their second-choice vote for a "mainstream" candidate. If the candidate has many sympathizers, it could lead to a surprise upset as voters can vote for anyone as their first choice without fear of unintended consequences.

RCV helps weed out extreme candidates as voters from a minority party or interest group can influence which candidate from a majority party or interest group wins.

RCV discourages negative campaigning. Suppose you’re ranking candidates A, B, and C. The race is close, and the winner will need some second-choice votes to reach the 50% threshold. You fully support candidate B as your first choice, but are uncertain how to rank A or C. Then candidate A says, "Candidate B eats puppies. Don’t vote for that puppy killer". Will that influence who gets your second-choice vote?

RCV also works for multi-winner elections such as city councils, school boards, and county supervisors, and achieves the goal of giving each interest group a fair share of power. See the example below.

The links page has more on RCV and where it is used now.

Choose 1 winner from 3 candidates

Round 1

12 Votes

10 Votes

8 Votes

One of the goals is to build consensus Nobody got a majority, so we continue to round 2. The blue candidate got the fewest votes and is eliminated. The computer now counts everyone’s votes again, this time using the second-choice votes of everyone who selected blue as their first choice. 6 of them selected orange as their second choice, 2 selected gray.

Round 2

14 Votes
 

16 Votes
The Winner

Eliminated
 

If there are more than three candidates, the process would repeat as needed. One candidate is eliminated at the end of each runoff round, and all votes are counted again in each following runoff round until one candidate gets over half the votes.

Majority Control with Minority Representation
If you’re not at the table, you’re on the menu

A multi-winner RCV election uses the same principles but has an additional goal of fairly allocating power among the various interest groups.

The first step is to decide who gets a seat at the table, and how many seats each interest group should get. If the largest interest group includes 3/5ths of the voters, and 2 smaller interest groups each include 1/5th of the voters, we would expect the largest group to get 3 of 5 council seats for majority control, and the other 2 groups to each get one seat for minority representation. Power is fairly allocated among the various groups. It’s important to understand that the groups are fluid and divisions may change from one election to the next. One election, the groups might be based on ethnicity. The next election the divisions may be philosophical differences about a community issue that spans ethnic lines.

If there are more interest groups than seats, only the larger groups get a seat, but everyone has a say about all the candidates. Smaller groups might build consensus by ranking candidates in a similar way, and together select one winning candidate.

We want to set the minimum votes needed to win a seat appropriately to provide a fair share of power to everyone. If we make the winning threshold too small, there could be 4 winners for 3 seats. If we make it too big, it’s harder for minority groups to get a seat at the table and a bare majority (51%) is less likely to elect a majority of the representatives. The vote-counting computer precisely calculates the optimal winning threshold as 1/(n+1) + 1 where n is the number of winners.

If electing 3 council members, any candidate getting (1/4 + 1) of the total votes is elected. A group with twice that many votes (1/2 + 2) could elect 2 candidates. A large interest group with 3 times the threshold (3/4+3), could fill all three seats.

What happens if a candidate gets more than the minimum votes needed? Suppose there are 3 like-minded candidates from a large interest group including 60% of the voters. Previously, we said that a large interest group including 60% of the voters should get 3 of 5 seats. What if the first-choice votes were very lopsided with 1 of the 3 candidates getting 50% of the first-choice votes, and the other two getting only 5%? If we eliminate the candidate with the fewest votes, we might eliminate a candidate from the large group we expect to produce 3 winners. Furthermore, the 50% voting for the same candidate would likely prefer either of the other 2 similar candidates over any others.

RCV solves this problem with some 5th-grade math such as fractions, percentages, and decimal places. If you’re not interested in the details, skip ahead to the example. We go back to the winning threshold. Any votes over this amount are a surplus. The winning candidate keeps just enough votes to win and the surplus votes are allocated to other candidates based on the second-choice preferences of everyone who voted for the winning candidate. Each voter has one vote, but that vote can be split among multiple winners based on calculations by the computer to achieve our goals of fair representation and treating everyone equally. Hand counting is possible using simpler, less precise methods.

Multi-winner RCV builds consensus, allocates power fairly, and gives everyone a say about all the winners. It also makes gerrymandering irrelevant as power is automatically distributed among interest groups, not accrording to district boundaries. Multi-winner RCV could be used to elect United States congress members by switching from single-member congressional districts to multi-member districts.

Choose 3 winners from 5 candidates
The Orange Clique vs. the Blue Clique

50 voters total: 30 blue, 20 orange 13 votes are needed to win (1/4 of 50 + 1).

The predicted result is two blue winners and one orange winner to give fair representation to everyone and maintain majority control for the blue clique (30 of 50 votes or 60%), with minority representation for the orange clique (20 of 50 votes or 40%).

Round 1

11 Votes
 

9 Votes
 

16 Votes
Winner

8 Votes
 

6 Votes
 

The blue/orange candidate got 16 votes which is enough to be elected, with 3 votes to spare. If we stopped here, the winners would be the blue/orange, orange/red, and orange/brown candidates which violates the goal of fair representation as the minority orange clique would have 2 representatives and the majority blue clique only one. We’ll keep going to find the next 2 winners. The 3 surplus blue/orange votes now transfer to another candidate based on each voter’s second choice. 10 of the 16 blue/orange voters selected the blue/purple candidate as their second choice. The other 6 blue/orange voters selected the blue/gray candidate as their second choice.

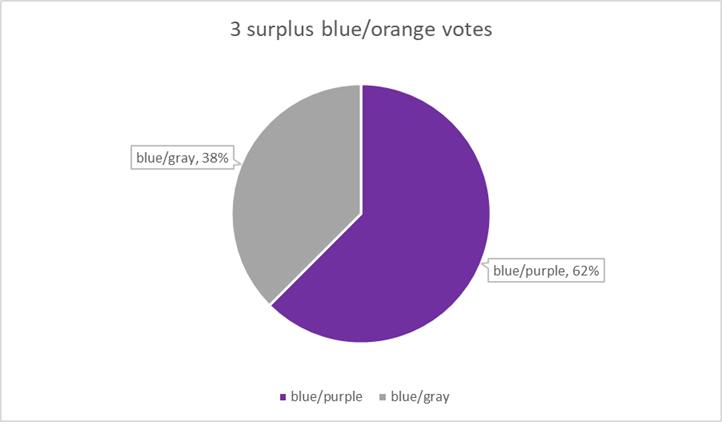
The computer can calculate this vote split precisely as (62.5% of 3) votes for the blue/purple candidate, and (37.5% of 3) votes for the blue/gray candidate. We’ll approximate that in the example below as 2 more votes for the blue/purple candidate and 1 more vote for the blue/gray candidate. Note that the total number of votes stays the same, and each voter has exactly 1 vote.

Round 2

11 Votes
 

9 Votes
 

13 Votes
Winner

10 Votes
 

7 Votes
 

Still no second winner as no other candidate got more than the required 13 votes. The computer follows the next RCV rule and eliminates the candidate with the fewest votes. In this example, the blue/gray candidate is eliminated, and the computer looks at the second-choice votes of all the blue/gray voters. All the blue/gray voters selected the blue/purple candidate as their next choice which makes blue/purple the next winner.

Round 3

11 Votes
 

9 Votes
 

13 Votes
Winner

17 Votes
Winner

Eliminated

Now we’re down to just orange candidates. The computer continues following the RCV rules to find the third winner, one of the orange candidates.